Boo-BKing.

下雨 最爱听的旋律

发表于 更新于 分类于
本文字数： 421 阅读时长 ≈ 1 分钟

题目描述

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

例如，给定一个 3叉树 :

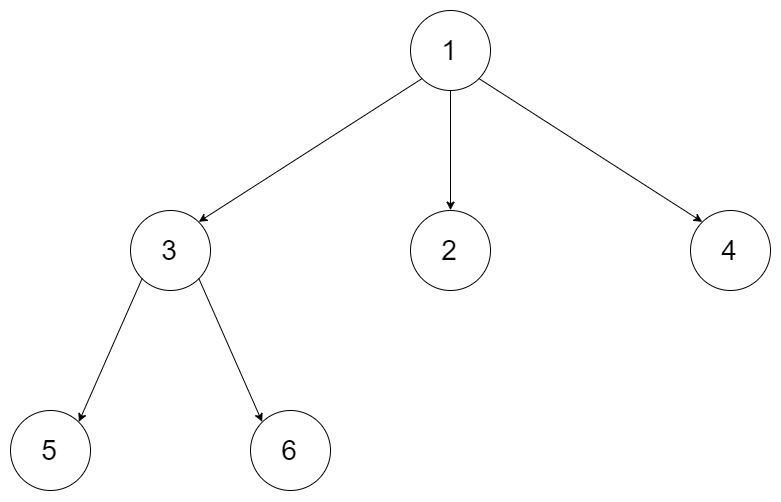
我们应返回其最大深度，3。

说明:

  1. 树的深度不会超过 1000。
  2. 树的节点总不会超过 5000。

python code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""

class Solution:
    def maxDepth(self, root: 'Node') -> int:
        if not root:
            return 0
        res = 0
        for c in root.children:
            res = max(self.maxDepth(c), res)
        return res + 1

发表于 更新于 分类于
本文字数： 617 阅读时长 ≈ 1 分钟

题目描述

给定长度为 2n 的整数数组 nums ，你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), …, (an, bn) ，使得从 1 到 n 的 min(ai, bi) 总和最大。

返回该 最大总和 。

1
2
3
4
5
6
7
8
9
10
11
12
13
示例 1：
输入：nums = [1,4,3,2]
输出：4
解释：所有可能的分法（忽略元素顺序）为：
1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
   所以最大总和为 4
   
示例 2：
输入：nums = [6,2,6,5,1,2]
输出：9
解释：最优的分法为 (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9

提示：

1
2
3
1 <= n <= 104
nums.length == 2 * n
-104 <= nums[i] <= 104

python code

1
2
3
class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        return sum(sorted(nums)[::2])

发表于 更新于 分类于
本文字数： 1.2k 阅读时长 ≈ 1 分钟

题目描述

给定一个二叉树，计算 整个树 的坡度 。

一个树的 节点的坡度 定义即为，该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话，左子树的节点之和为 0 ；没有右子树的话也是一样。空结点的坡度是 0 。

整个树 的坡度就是其所有节点的坡度之和。

示例 1：

1
2
3
4
5
6
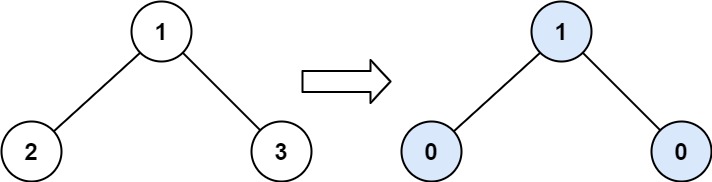
7
输入：root = [1,2,3]
输出：1
解释：
节点 2 的坡度：|0-0| = 0（没有子节点）
节点 3 的坡度：|0-0| = 0（没有子节点）
节点 1 的坡度：|2-3| = 1（左子树就是左子节点，所以和是 2 ；右子树就是右子节点，所以和是 3 ）
坡度总和：0 + 0 + 1 = 1

示例 2：

1
2
3
4
5
6
7
8
9
10
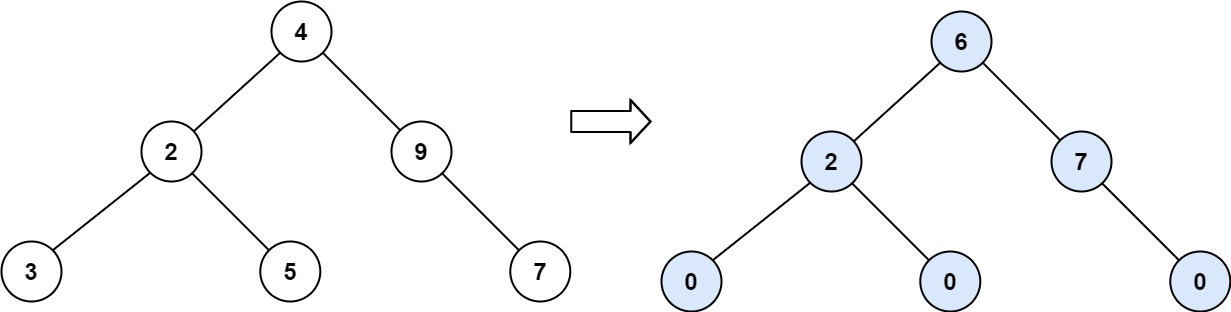
输入：root = [4,2,9,3,5,null,7]
输出：15
解释：
节点 3 的坡度：|0-0| = 0（没有子节点）
节点 5 的坡度：|0-0| = 0（没有子节点）
节点 7 的坡度：|0-0| = 0（没有子节点）
节点 2 的坡度：|3-5| = 2（左子树就是左子节点，所以和是 3 ；右子树就是右子节点，所以和是 5 ）
节点 9 的坡度：|0-7| = 7（没有左子树，所以和是 0 ；右子树正好是右子节点，所以和是 7 ）
节点 4 的坡度：|(3+5+2)-(9+7)| = |10-16| = 6（左子树值为 3、5 和 2 ，和是 10 ；右子树值为 9 和 7 ，和是 16 ）
坡度总和：0 + 0 + 0 + 2 + 7 + 6 = 15

示例 3：

1
2
输入：root = [21,7,14,1,1,2,2,3,3]
输出：9

提示：

  • 树中节点数目的范围在 [0, 104] 内
  • -1000 <= Node.val <= 1000

算法

(深度优先遍历，DFS) O(n)
遍历过程中，分别递归遍历左子树和右子树，分别取得它们的结点总和，并累计答案。然后将自身结点的值和左右子树结点的总和累加到一起返回。

时间复杂度

每个结点仅遍历一次，故时间复杂度为 O(n)

python code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.ans = 0

    def dfs(self, root):
        if not root: return 0
        l = self.dfs(root.left)
        r = self.dfs(root.right)
        self.ans += abs(l - r)
        return root.val + l + r
    
    def findTilt(self, root: TreeNode) -> int:
        self.dfs(root)
        return self.ans

发表于 更新于 分类于
本文字数： 401 阅读时长 ≈ 1 分钟

题目描述

给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的个数。

示例 1 :

1
2
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。

说明 :

  1. 数组的长度为 [1, 20,000]。
  2. 数组中元素的范围是 [-1000, 1000] ，且整数 k 的范围是 [-1e7, 1e7]。

python code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        res = {0: 1}
        ans = 0
        preSum = 0
        for num in nums:
            preSum += num
            if preSum - k in res:
                ans += res[preSum-k]
            if preSum in res:
                res[preSum] += 1
            else:
                res[preSum] = 1
        return ans

发表于 更新于 分类于
本文字数： 870 阅读时长 ≈ 1 分钟

题目描述

给定两个非空二叉树 s 和 t，检验 s 中是否包含和 t 具有相同结构和结点值的子树。s 的一个子树包括 s 的一个结点和这个结点的所有子孙。s 也可以看做它自身的一棵子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
样例
给定的树 s:

     3
    / \

   4   5
  / \
 1   2

给定的树 t：

   4 
  / \
 1   2

返回 true，因为 t 与 s 的一个子树拥有相同的结构和节点值。
给定的树 s：

     3
    / \

   4   5
  / \
 1   2
    /
   0

给定的树 t：

   4
  / \
 1   2

返回 false。

算法

(暴力遍历) O(nm)
思路很简单，对于 s 的每一个结点，都尝试与 t 进行匹配，此操作递归进行即可。
匹配时，仍然需要递归匹配当前 s 中的子树和 t 的每一个结点。

时间复杂度

s 的每个结点都需要 O(m) 的时间匹配，故总时间复杂度为 O(nm)。

python code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSame(self, s, t):
        if not s and not t: return True
        if not s or not t: return False
        if s.val != t.val: return False
        return self.isSame(s.left,t.left) and self.isSame(s.right, t.right)

    def isSubtree(self, s: TreeNode, t: TreeNode) -> bool:
        if not s: return False
        return self.isSame(t,s) or self.isSubtree(s.left,t) or self.isSubtree(s.right, t)

发表于 更新于 分类于
本文字数： 0 阅读时长 ≈ 1 分钟

发表于 更新于 分类于
本文字数： 0 阅读时长 ≈ 1 分钟

发表于 更新于 分类于
本文字数： 0 阅读时长 ≈ 1 分钟

发表于 更新于 分类于
本文字数： 0 阅读时长 ≈ 1 分钟